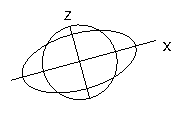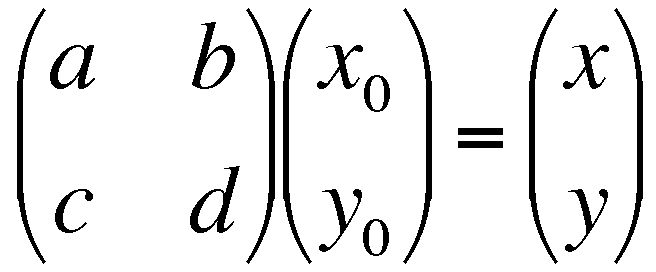Material on this page is copyright © 2016 John W.F. Waldron
Kinematics: Deformation and Strain
Deformation basics
Deformation and strain
Components of deformation
Kinematic analysis includes four components of deformation
- translation (change in position)
- rotation (change in orientation)
- dilation (change in size) and
- distortion (change in shape)
Translation and rotation are grouped as rigid body deformation, whereas dilation and distortion constitute strain.
In practice, dilation is very difficult to measure in most rocks, and so normally when we speak of strain we are speaking of distortion.
Why measure strain?
Many of the features we see in deformed rocks are products of strain. It is important to have some understanding of strain to answer questions like:
- How much shortening has there been in the Cordillera?
- How is fabric produced by deformation?
- How can we figure out original thicknesses of strata affected by folds and cleavage?
- When we see a major mylonite zone, how much movement has there been?
- Can we trust sedimentary structures and paleocurrent directions measured in deformed rocks?
- How much distortion accompanied folding in a foothills oilfield, and how did this affect porosity?
All these are questions that can only be answered with an understanding of strain.
Strain markers
Many rocks contain evidence for strain. To actually measure strain we need strain markers: features that had an original shape or size that we can guess, so we can use them to estimate distortion.
Homogeneous and heterogeneous strain
Homogeneous strain is strain that produces the same distortion everywhere. As a result, straight lines stay straight, and parallel lines stay parallel.
Heterogeneous strain is involves distortion or dilation that varies from place to place. Straight lines do not in general stay straight; parallel lines do not in general stay parallel.
When strain is systematically heterogeneous between different components of a rock (e.g. garnets are rotated but quartz is flattened) we describe the strain as partitioned.
Homogeneous strain is much easier to deal with and we will start our study of strain with homogeneous strain. Where we encounter heterogeneous strain, we will still be able to use the concepts and terminology of homogeneous strain by either
- looking at a single point or very small element, or
- by averaging out all the variations and looking at the bulk strain
Strain compatibility
Another phenomenon that helps us understand deformation is strain compatibillity. When rocks deform by ductile processes, it is unusual for large empty spaces to open up within rocks, because of overburden pressure. Hence, the strained portions of a rock have to fit together without leaving any spaces. This limits the types of strain heterogeneity that can occur.
Clearly, not all deformed rocks satisfy strain compatibility. A fault breccia, for example, may contain large open spaces. On the other hand, at large scale, strain compatibility is an important concept in the balancing of cross-sections through thrust belts, so it has applications in both brittle and ductile deformed rocks.
Finite strain, incremental strain, instantaneous strain, and flow
Finite strain
Everything we have said so far compares a final state to an initial state. Typically, if we look at deformed objects as guides to strain, that's what we are doing. The strain involved is called the finite strain. A common measure of finite strain is extension, or fractional change in length, represented by the letter e. Another measure is the shear strain γ, a measure of the change in angle between two lines.
Strain paths, strain rate, and flow
In getting from starting state A to final state B, a rock passes through an infinite series of very small steps that make up its strain history. When we look at a deformed rock we see the results of the finite strain, but it is important to remember that there are infinitely many strain histories that could result in the same finite strain.
It is sometimes helpful to look at a very small part of the strain history, which is referred to as the incremental strain. Incremental strains may be represented by symbols such as δe or δγ
In strain theory, we sometimes consider an infinitesimally small increment of strain, which is referred to as instantaneous strain or infinitesimal strain, effectively the derivative of the finite strain.
For example, if finite strain is represented by an extension e or a shear strain γ then an instantaneous strain is de or dγ.
de/dt and dγ/dt (also written
,
) are strain rates - measures of the speed at which rocks flow.
The remainder of this section deals with finite strain; we return to the study of strain paths and flow in a later section.
Strain along lines
In dealing with strain in one dimension we usually focus on material lines. A material line can be thought of as a row of sand grains, or maybe a row of calcium atoms in a calcite crystal. It is a line of material particles (as opposed to a line that is just part of a geometrical construction.)
Longitudinal strain
Longitudinal strain means change in length. Suppose a material line starts off with length l0 and ends up with length l; we can measure its longitudinal strain in several ways.
extension
Extension e is also known as fractional change in length e = (l-l0)/l0
stretch
The stretch is the new length as a proportion of the old s = l/l0 = 1+e
quadratic elongation
λ = s2
natural strain
ε = ln(s)
Shear strain
 There is a second way that strain affects material lines. A line is subject to shear strain if adjacent particles of rock flowed past it in a parallel direction. For example, shear strain is occurring at present along the western margin of the North American plate as the Pacific Plate moves northward relative to the North American Plate
There is a second way that strain affects material lines. A line is subject to shear strain if adjacent particles of rock flowed past it in a parallel direction. For example, shear strain is occurring at present along the western margin of the North American plate as the Pacific Plate moves northward relative to the North American Plate
The easiest way to represent the shear strain along a line is to look for an originally perpendicular material marker line (e.g. in a deformed fossil)
After deformation we look at how much that marker has rotated out of perpendicular. Again there are several ways to represent the shear strain:
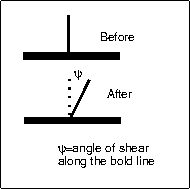
angle of shear
The angle is the angle of shear represented by the Greek letter psi ψ
engineering shear strain
Shear strain (sometimes called engineering shear strain, is represented by the Greek letter gamma γ = tan ψ
tensor shear strain
For some purposes it is easier to use the tensor shear strain represented by γ/2
Finite strain in 2 dimensions
Strain ellipse
Once we move into two dimensions, things are a bit more complicated. There is an infinite number of differently oriented material lines in a surface. Lines with different orientations will show different values of s and γ
The most intuitive way to represent strain in 2D is to imagine a circle before deformation, and to look at its shape after deformation. In general (for homogeneous strain) the circle will become an ellipse - the strain ellipse.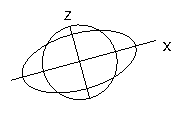
The strain ellipse is the product of a finite strain applied to a circle of unit radius. It is an ellipse whose radius is proportional to the stretch s in any direction.
A deformed circular object has the same shape (though not, strictly, the same size) as the strain ellipse.
Lines of no finite extension
If we superimpose the strain ellipse on the original unit circle, we can separate a field of finite extension from a field of finite shortening. These fields are separated by two lines of no finite extension or LNFE
Depending on the dilation and the shape of the strain ellipse the LNFE may be closer to the long axis or the short axis. If the strain involves a lot of dilation (negative or positive) then all lines may have positive or negative s, and there is no LNFE.
Strain axes
Like any other ellipse, there are two other special lines, the longest and shortest radii, known as strain axes, labelled X and Z or alternatively s1 and s3. (Notice that we are saving s2 and Y for the 3D case.)
The strain axes have another special property - the are perpendicular before and after deformation. So, they must be lines of zero shear strain. In general, they are the only two lines along which the shear strain is zero.
Describing a strain in 2D
Note that it takes 3 numbers to describe a finite strain in 2D: s1, s3, and the orientation of a strain axis (typically represented φ' ). (However, to describe deformation a fourth number is needed: we need to know how much the strain axes have rotated from the starting state to the final state.)
Strain ratio
The strain ratio Rs = s1/ s3 is called the strain ratio and is a measure of the overall intensity of distortion.
Dilation
Dilation Δ is the fractional change in area; it is positive if the area increases, negative if it decreases.
The product s1 x s3 is a measure of the area of the strain ellipse. It is used to measure the dilation according to the following formula:
1 + Δ = s1 x s3
Rotational and non-rotational deformation
Rotational component of deformation
Notice that if we want to extend our description to include the rotational part of deformation (relative to some material reference line like the trace of a horizontal bedding plane or the edge of a shear zone) then we need another measurement - this might be obtained from the orientation of the strain axis before and after deformation (φ, φ').
The difference ω = φ'- φ is a measure of how much overall rotation has occurred during deformation.
Non-rotational deformation or pure strain
Under some circumstances, we may envisage that the strain axes have the same orientation (relative to a reference direction) before and after deformation. Such a deformation is known as a pure strain because the rotation ω is zero. It is also sometimes called a non-rotational or irrotational deformation. There is a special type of pure strain, known (confusingly) as pure shear in which the dilation is also zero. Then we can say that
1 + Δ = s1 x s3 = 1
and therefore s3 = 1/s1
Rotational deformation
All other types of deformation are termed rotational. In such deformations the strain axes rotate during deformation. ω is non-zero.
In general, it is always possible to think of a finite rotational strain as a combination of a non-rotational, pure strain, combined with a simple rotation. (Remember though, that because we are dealing with finite strain, it's not possible using the techniques of this section to say whether the rotation occurred before, during, or after the strain. Often, we assume that rotation and distortion were occurring at the same time, but this is not necessarily the case.) Also note that if we choose our reference direction to coincide with a strain axis, then any finite strain appears non-rotational.
One special case of rotational deformation, simple shear, is of common interest in the study of shear zones and folds. This is a non-dilational strain in which one LNFE is not rotated. Simple shear can easily be simulated by drawing on the side of a deck of cards and then shearing the deck of cards. It is also easily simulated using the shear transformation in CorelDraw, Illustrator, or other drawing program.
Variation of strain with direction
Examples
In strain analysis we often are able to measure s or γ in a few directions, and would like to reconstruct the whole strain ellipse from these data.
[Examples shown in the lecture may include: belemnites; fold and boudinage of veins; veins and stylolites; deformed trilobites; deformed graptolites]
Graphs
To do this, we need to know how s and γ vary with direction in the deformed rock. We measure the direction φ' clockwise from the s1 (X) axis, in the deformed rock.
For simplicity, let's deal with a pure strain, so that we don't have to worry about rotation.
The graph of s or e plotted against φ' looks like a distorted cosine curve.
We can also plot a graph of shear strain against φ'
This also looks a bit like a sine wave at low strains, but becomes more distorted at higher strain ratio R.
[These graphs are known as Breddin graphs: examples will be shown in the lecture]
In general the mathematical form of these curves makes them rather cumbersome to deal with.
Mohr circle for strain
It turns out that there's a simplification that can be achieved if we define two new quantities, based on the square of the stretch (also known as the quadratic elongation) λ.
The values of λ along the strain axes are λ1 and λ3.
λ' is defined as 1/λ and γ' is defined as γ/λ
Then
and
These are equations of a circle with radius (λ'3 - λ'1)/2 with centre at (λ'3 + λ'1)/2
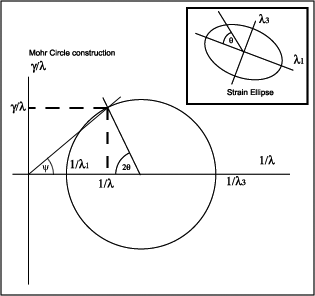
Notice how any point on the Mohr circle describes the state of strain on a line in the strained rock. It is easy to convert from λ' and γ' to the more useful quantities s and γ, and vice versa. Notice also that angles φ' measured in the rock are represented by points on the circle that are at an angle 2φ' around the Mohr circle. The two strain axes, 90° apart in the rock, are located 180° apart on the circle. Notice that γ', and therefore γ, is zero (as it should be) at both these axes.
In addition, the angle marked ψ on the diagram has to be tan-1(γ'/λ') = tan-1γ, or the angle of shear ψ.
Because it can be easily constructed with a compass, the Mohr circle construction is very useful for determining longitudinal strain and shear strain in any given direction, provided the principal strains are known.
Deformation matrix
Definition
So far we have met two methods for representation of finite strain in 2D. These are the Mohr circle and the strain ellipse. We now introduce a third representation, that is actually the basis for all the theory of the strain ellipse and the Mohr circle. This is a 2 x 2 matrix of 4 numbers known as the deformation gradient tensor, or more simply as the deformation matrix and commonly represented with a bold F.
- We can draw a unit square, and set up some axes so that it is at the origin of a graph. The square will have two diagonally opposite corners at coordinates (1,0) and (0,1).
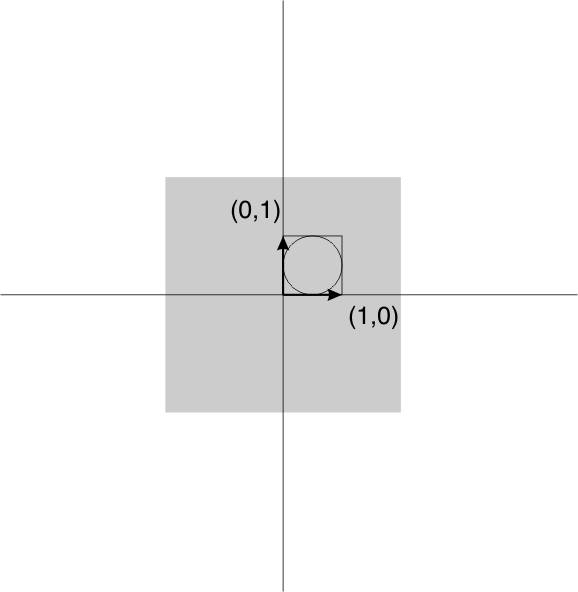
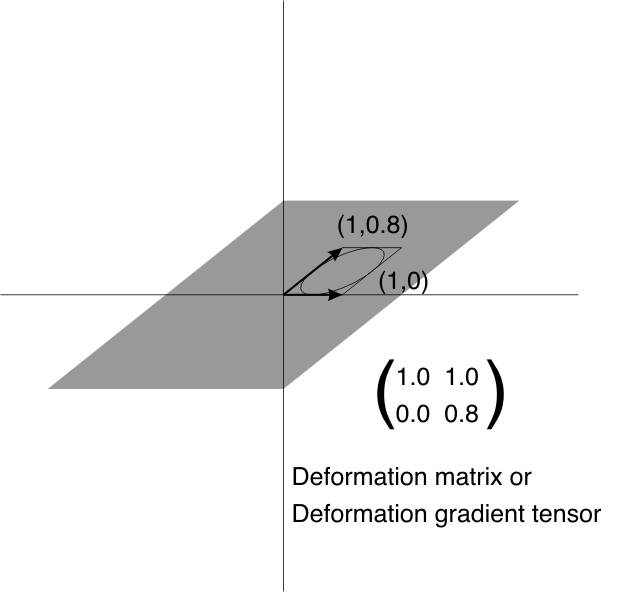
- After deformation the square will be a parallelogram. The coordinates of the two diagonally opposite corners are used to fill the deformation matrix, also known as the deformation gradient tensor.
Using the deformation matrix to simulate strain
If a vector is used to represent the coordinates of any point in space, and deformation is represented by a matrix F, then matrix multiplication may be used to find the effect of deformation on that point.
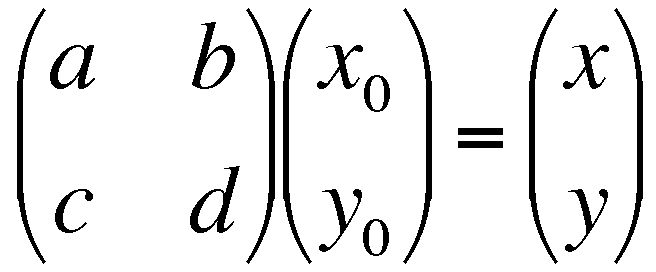
This can also be written Fx0= x
Strain parameters from the deformation matrix
Rotation ω is given by tan(ω) = (c-b) / (a+d)
Dilation Δ is given by 1 + Δ = ad-bc
Strain ratio: sadly this formula is not so simple!
Measuring strain in 2D
We now have enough information to deal with practical measurement of strain from rocks. It's important to remember that any strain determination is dependent on some assumptions about the starting state of the rock.
Because the starting rock can no longer be examined, these assumptions are always difficult to test in real rocks.
In strain analysis the best strategy is to use 2 or more different techniques, based on different assumptions, and see if they give the same answer.
Direct measurement of elliptical objects
This is the simplest case. If we have an object that was perfectly circular before deformation, we can measure its shape to obtain the shape of the strain ellipse.
The starting assumptions are
- The objects were initially spherical
- They deformed homogeneously with the matrix
The most likely objects are volcanic lapilli, and reduction spots. (Limestone ooids are sometimes very close to circular. However, they are less likely to deform homogenenously with their matrix, because they often have slightly different texture or composition than the surrounding material.)
Because we typically have no control over original size, this method can only tell us about distortion, not dilation.
Direct measurement of longitudinal strain
Linear objects are sometimes available, in circumstances where we can reconstruct the length before deformation. For example, very rigid elongated objects such as belemnite fossils and toumaline crustals may undergo boudinage during strain. It is possible to determine the original length of the object by adding up the lengths of all the boudins. The final length can be measured directly, and the stretch can be calculated (l/l0).
Once several objects have been measured, their orientations and lengths can be plotted (in radial coordinates). A best fit ellipse may be estimated using a set of elliptical templates. In theory a minimum of three points may constrain the ellipse but usually more are advisable.
The assumptions for this method are:
- There is no distortion of the boudins
- The separation of the boudins represents the whole of the longitudinal strain.
If these assumptions are satisfied, this method can in theory yield both the dilational and distortional components of the strain ellipse.
Measurement of shear strain: Mohr circle and Wellman methods
Often, we can measure shear strains more easily than longitudinal strains. This is particularly the case with bilaterally symmetrical fossils, which have been distorted by strain. A minimum of two, differently oriented fossils is necessary. If only two or three fossils are available, a Mohr circle construction is typically used. For multiple measurements we use a construction called a Wellman plot.
Mohr method
For the Mohr construction, plot the circular part of a Mohr diagram at arbitrary size on tracing paper. Draw two radii representing the lines along which shear strain is known; the angle between the radii must be double the angle in the rock (because angles are doubled in the Mohr construction). Next, plot the axes on graph paper, and draw lines from the origin inclined at angles ψ to the horizontal axis. Then superimpose the tracing paper on the graph paper to complete the construction, making sure that corresponding lines intersect.
Assumptions for this method:
- Original shape of fossils is known
- Fossils have deformed homogeneously with their matrix
This method yields only the shape (distortion component) and not the size (dilation component) of the strain ellipse.
Wellman method for bilaterally symmetric fossils
Note: this method is not required for this year; it is retained here for interest.
For the Wellman plot, first draw on tracing paper a horizontal reference line. For each fossil, measure the orientations of two originally perpendicular lines. Draw lines with the same orientation, starting at each end of the reference line (4 lines in all, forming a parallelogram). Mark the corners of the parallelogram. Repeat for each fossil. The marked points should fall on a strain ellipse that has the reference line as a radius.
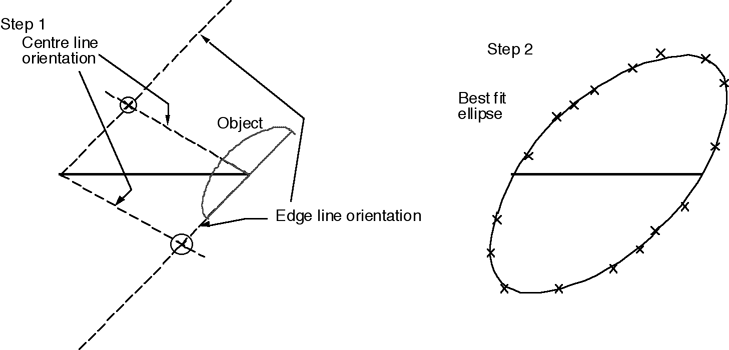
Assumptions for this method:
- Original shape of fossils is known
- Fossils have deformed homogeneously with their matrix
This method yields only the shape (distortion component) and not the size (dilation component) of the strain ellipse.
Rf/φ methods
A common problem in strain analysis may be that the only available markers were elliptical, not circular, even before deformation. We can attempt to overcome this with a plot known as an Rf/φ plot.
Rf is the ellipticity of a measured object (e.g. the ratio of long axis to short axis of a deformed pebble.). Rf can be thought of as a combination of an initial ellipticity Ri and a strain ellipticity Rs.
Phi is the orientation of the long axis of the object, with respect to some reference direction (e.g. north, or in a vertical section, horizontal.)
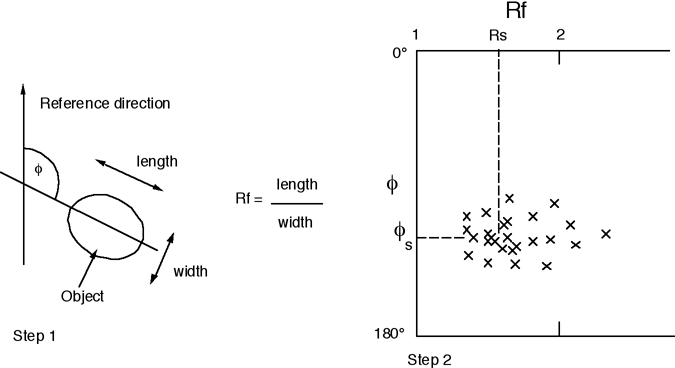
In the plot, each point is plotted on axes Rf and φ, typically producing a scattered cluster. The densest part of the cluster, somewhere in the centre, represents the φ value of the S1 axis. The value of Rs is represented by Rf at the densest part of the cluster. Sets of standardized curves are available for estimating Rs.
Assumptions for this method:
- The variably-shaped objects were randomly oriented before deformation
- Obects have deformed homogeneously with their matrix
[Alternatively, the measurements can be plotted on a hyperbolic net, in which φ is measured as an angle and Rf is plotted as a distance from the centre. The net is rotated so that its line of symmetry bisects the cluster. The net also shows a set of hyperbolic lines; the line which bisects the cluster is chosen, and the value of R at its closest approach to the origin is an estimate of Rs.]
Fry's method
There are many examples of rocks in which the only strain markers are objects which are expected not to have deformed homogeneously with their matrix. Examples include pebbles in conglomerates with a soft matrix, sand grains or ooids that have become sutured by stylolytic contacts, etc.
In these cases, the shapes of the objects cannot be used to determine strain. Instead, it may be possible to use the spacing of the objects. This method works if the objects were uniformly spaced in all directions before deformation, or if they were at least, statistically uniform in their spacing; we say the objects were anticluster. (What this means is that it's possible to identify an average or typical spacing of nearest objects, measured centre to centre, in the undeformed rock.)
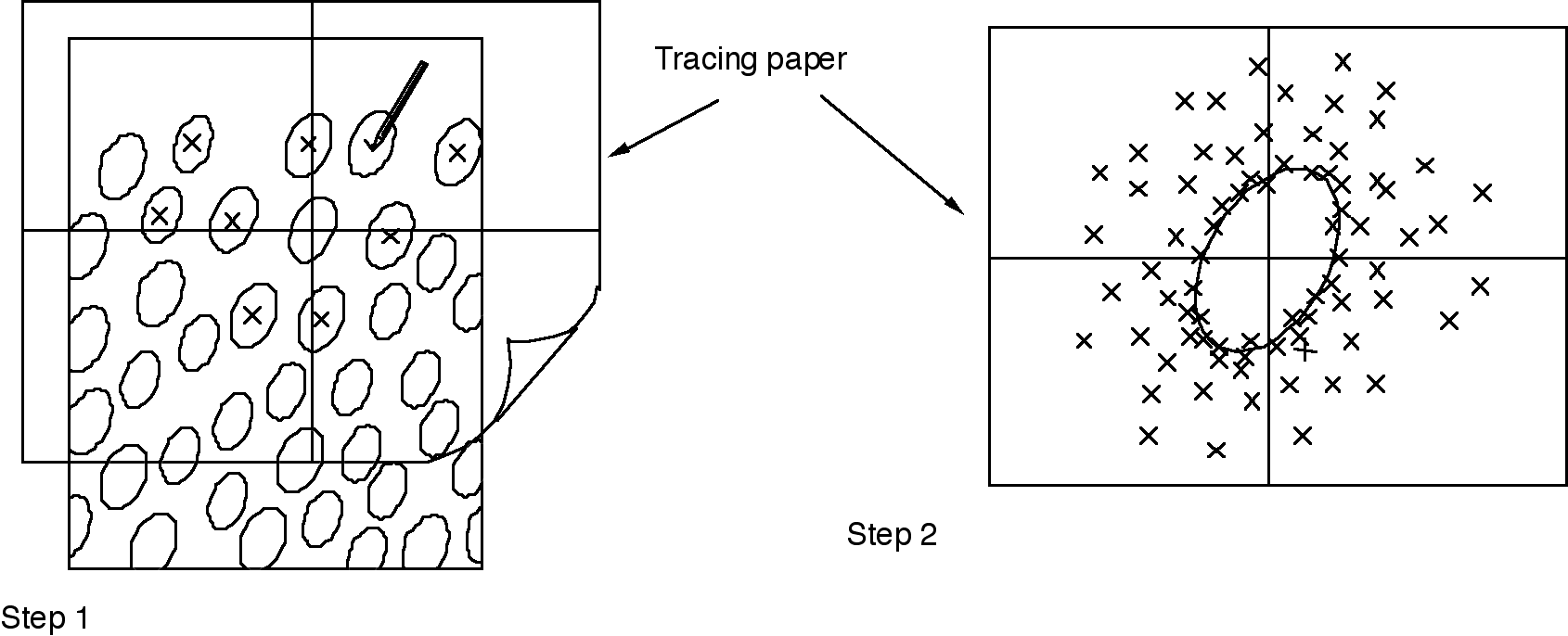
The procedure involves tracing paper. Mark an x or a set of axes on tracing paper. Place the origin over one object. Mark the centres of all nearby objects. Move the tracing paper to the next object (without rotating it). Repeat the procedure.
After a sufficient number of objects has been traced (typically >50), an elliptical void may appear in the centre of the diagram. The shape of this void is the shape of the strain ellipse.
Assumptions for this method
- Objects were initially uniformly and isotropically distributed
- If objects were not spherical, they did not have a preferred original orientation
- Objects have not slid past each other during deformation
Unless the original size of objects can be estimated (rarely possible) this method gives only the shape (distortion component) of the strain ellipse.
Finite strain in 3D
Representing strain in 3D
Strain ellipsoid
When we move into 3 dimensions we can use analogous measures of strain to those in two dimensions.
The 3D equivalent of the strain ellipse is the strain ellipsoid. This is the product of deformation applied to a unit sphere.
Cross-sections of the strain ellipsoid are strain ellipses (these can include circular cross-sections)
In general, the way we determine the 3D strain ellipsoid is to saw up rocks to define surfaces on which we find 2D strain ellipses. Then recombine the ellipses into an ellipsoid.
Strain axes and principal planes of strain
The orientation of the strain ellipsoid is indicated by the directions of three mutually perpendicular strain axes, which are, in general, the only three lines that are mutually perpendicular before and after deformation.
The strains along the strain axes are the three principal strains. The principal stretches are s1 > s2 > s3 or X, Y, and Z
Lines of no finite extension typically lie in a cone
The three strain axes are poles to three principal planes of strain, which are, in general, the only three planes that suffer zero shear strain.
Dilation
The volume dilation is given by 1+Δ = s1s2s3
Strain ellipsoid shapes
Axial ratios
In 2 dimensions we could specify the shape (distortion component) of the strain ellipse with a single number, the strain ratio.
In 3 dimensions that's not enough. There are many different shapes of strain ellipsoid
Typically we use two strain ratios to indicate the shape of the ellipsoid. They are conventionally
a = s1/s2 = X/Y
b = s2/s3 = Y/Z
Notice that the minimum value of a and b is 1.0, from the definition.
Flinn plot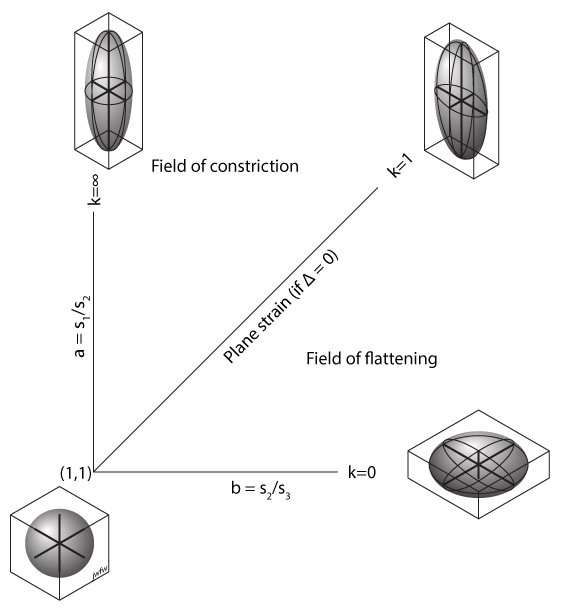
We can make a plot of a against b, on which the shape of any strain ellipsoid is represented as a point. This is known as a Flinn plot. Note that the origin is at (1,1) not (0,0) because the minimum value of a strain ratio is 1 by definition.
An alternative plot, known as the logarithmic Flinn plot or Ramsay plot, shows log(a) against log(b). Its origin is at (0,0).
Strain ellipsoid shapes
The ratio a/b, known as k, is an indication of the overall symmetry of the strain ellipsoid. Values of k greater than 1 characterize ellipsoids with one long axis and two shorter ones s1 >> s2 > s3, informally known as cigars. Values of k less than 1 characterize ellipsoids with two long axes and one shorter one s1 > s2 >> s3, informally known as pancakes.
Constriction
If s1 >> s2 = s3 then the strain is described as axially symmetric constriction. k is infinite.
Flattening
If s1 = s2 >> s3 then the strain is described as axially symmetric flattening. k is zero.
Plane strain
Between the field of cigars (constriction) and the field of pancakes (flattening) is a line where k=1.
If k=1 and we additionally know there is no volume change, then it is easy to prove that
Under these circumstances the only movements of particles (particle paths and flow lines) due to distortion are in the s1 s3 plane. We can represent this strain as if it were a 2D strain. This type of strain is called plane strain and is a common assumption in section balancing.
Progressive strain and flow
....is now covered in a separate section
 There is a second way that strain affects material lines. A line is subject to shear strain if adjacent particles of rock flowed past it in a parallel direction. For example, shear strain is occurring at present along the western margin of the North American plate as the Pacific Plate moves northward relative to the North American Plate
There is a second way that strain affects material lines. A line is subject to shear strain if adjacent particles of rock flowed past it in a parallel direction. For example, shear strain is occurring at present along the western margin of the North American plate as the Pacific Plate moves northward relative to the North American Plate