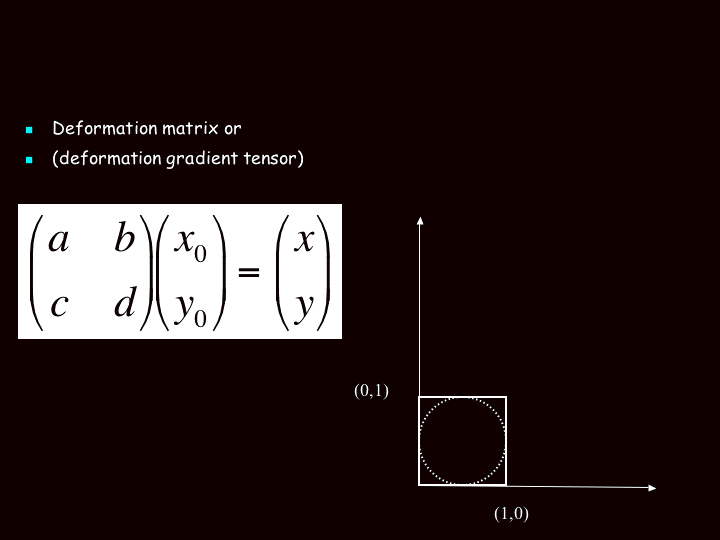
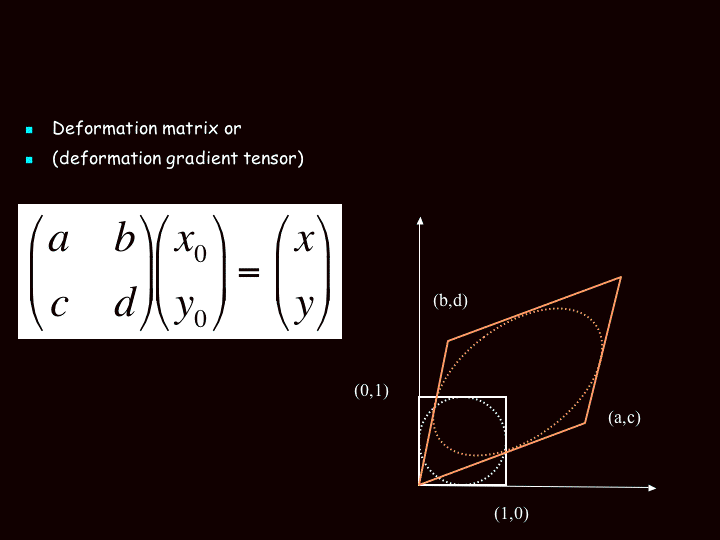
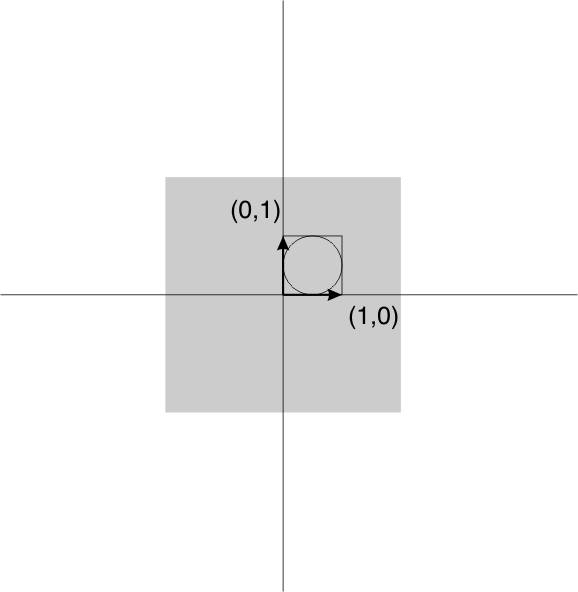
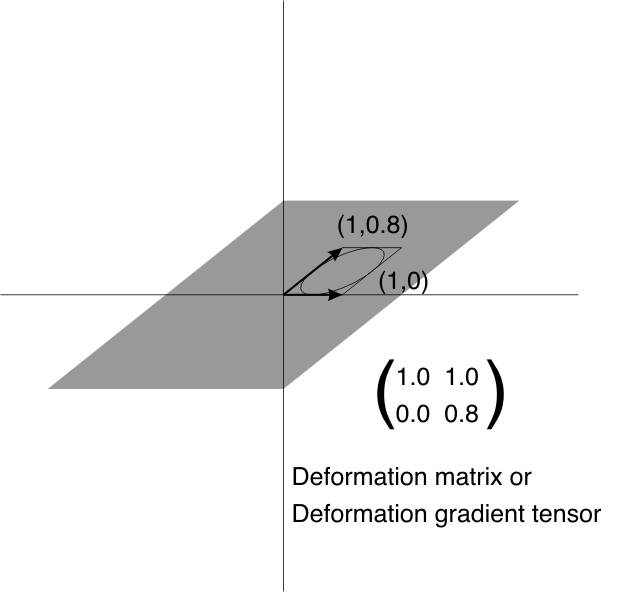
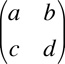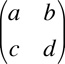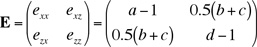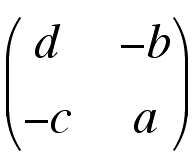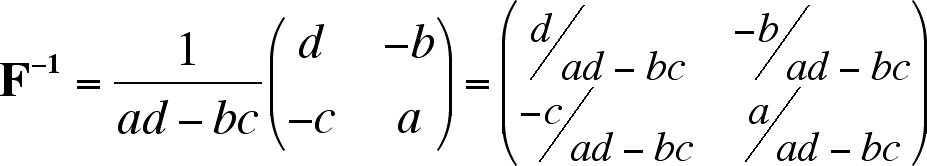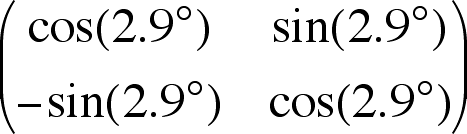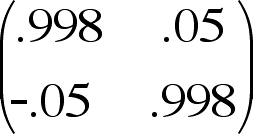Principle of the deformation matrix (deformation gradient tensor); before and after strain.
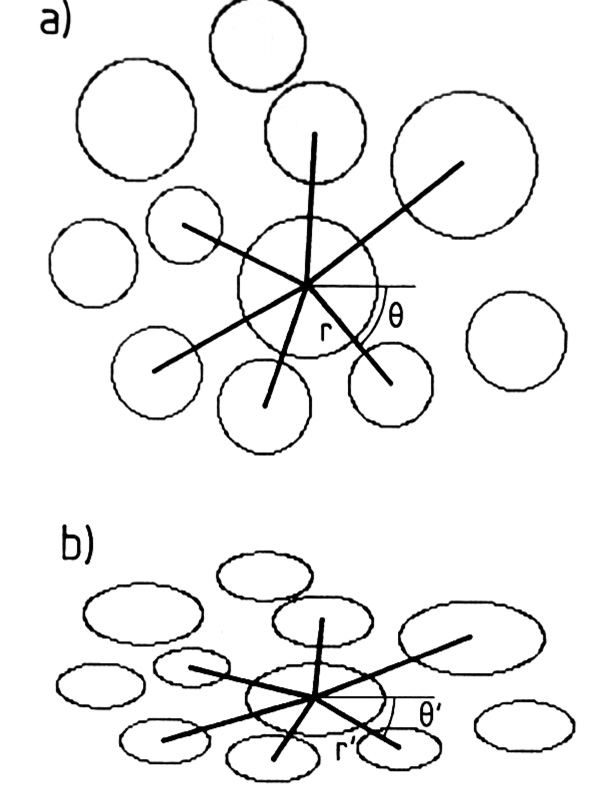
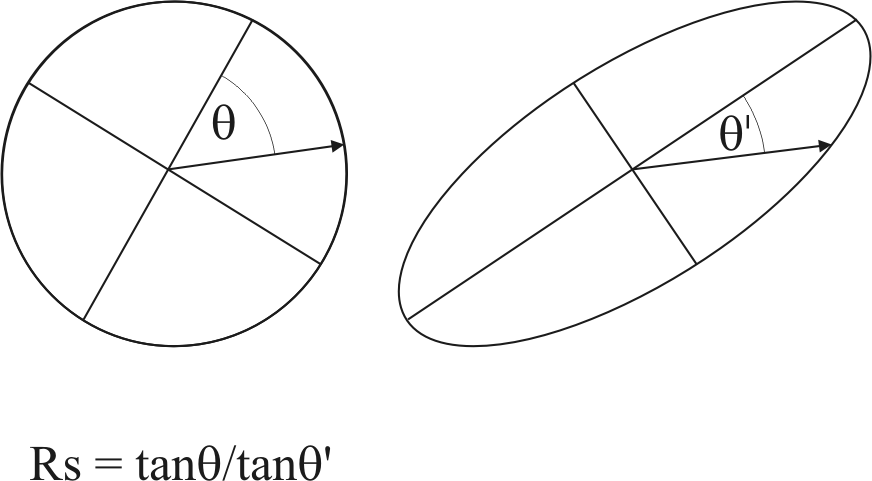
Variation of strain with direction. Ramsay, J. G., and Huber, M. I., 1983, The Techniques of Modern Structural Geology. Volume 1: Strain Analysis: London, Academic Press, 307 p. Reproduced under license from Cancopy; further reproduction prohibited.
 |
 |
|
|
 |
|
|
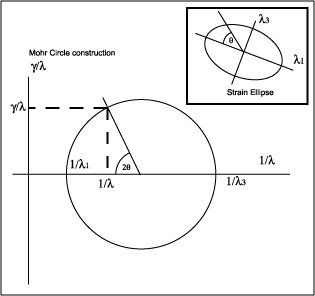
| Top left: Variation of stretch with direction
Top right: Variation of shear angle with direction
Lower left: Mohr circle construction for finite strain
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| As an alternative to the strain ellipse we can use a matrix to describe deformation |
|
|
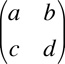 |
|
|
| We define matrix multiplication as follows: |
|
|
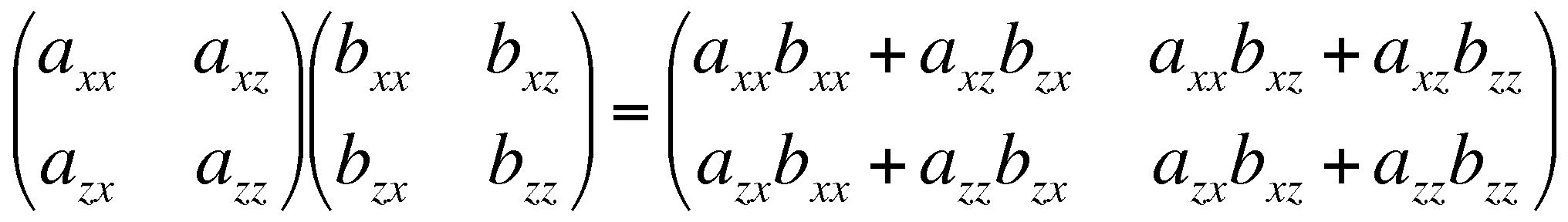 |
|
| If a vector is used to represent the coordinates of a point in space, then matrix multiplication may be used to transform that point to a new location. |
|
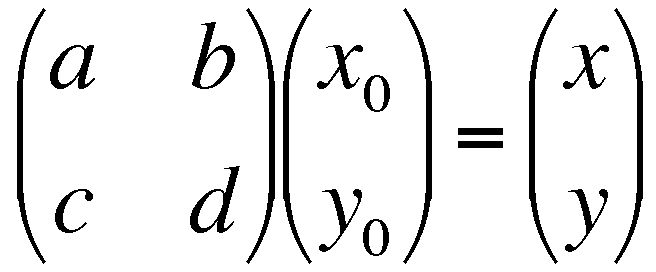 |
|
|
| This can also be written Fx0 = x |
|
|
|
|
|
|
|
|
|
|
Some special cases
 The matrix that does nothing
The matrix that does nothing
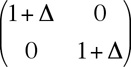 A matrix that describes a simple dilation
A matrix that describes a simple dilation
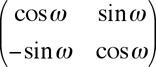 A rotation clockwise about the origin
A rotation clockwise about the origin
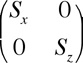 A pure strain with strain axes parallel to x and y
A pure strain with strain axes parallel to x and y
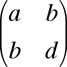 A general pure strain
A general pure strain
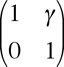 A simple shear parallel to x
A simple shear parallel to x
|
|
|
Converting the deformation matrix back to a strain ellipse
|
|
|
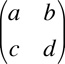 |
The dilation is given by
1+Δ = ad-bc
|
|
|
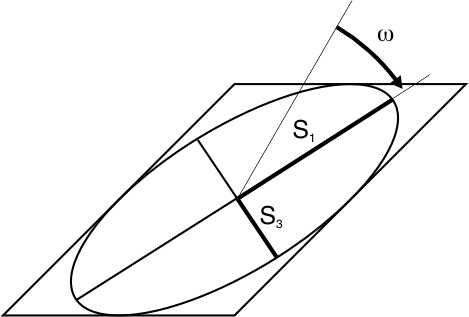
The rotational component of deformation is given by
tanω =(b-c)/(a+d)
|
|
|
The orientations of the strain axes are given by
-tan2θ'=2(ac+bd)/(a2+b2-c2-d2) where θ' = angle of a strain axis clockwise from axis x after deformation.
|
|
|
|
 |
|
|
The principal strains are given by the two solutions to the following
λ=0.5{a2+b2+c2+d2 + √[(a2+b2+c2+d2)2 - 4(ad-bc)2]}
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Converting the strain ellipse to a deformation matrix
|
|
|
|
For strain ellipse with principal stretches S1, S3.θ is initial clockwise angle of S1 from x axis; θ' is clockwise angle of S1 from x axis after deformation
|
|
|
|
 |
|
|
|
a = S3 sinθ' sinθ + S1 cosθ' cosθ
b = S3 sinθ' cosθ - S1 cosθ' sinθ
c = S3 cosθ' sinθ- S1 sinθ' cosθ
d = S3 cosθ' cosθ +S1 sinθ' sinθ
|
|
|
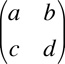 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Other matrices that relate to strain
|
|
|
|
The displacement gradient tensor J is related to the deformation matrix, very simply:
J = (F - δ) =
When a point x is multiplied by J, the result is a vector describing the displacement of x (ie its change in location).
Jx0 = x - x0
|
|
|
Strain tensor E
|
|
|
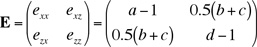 |
|
|
|
|
|
|
|
|
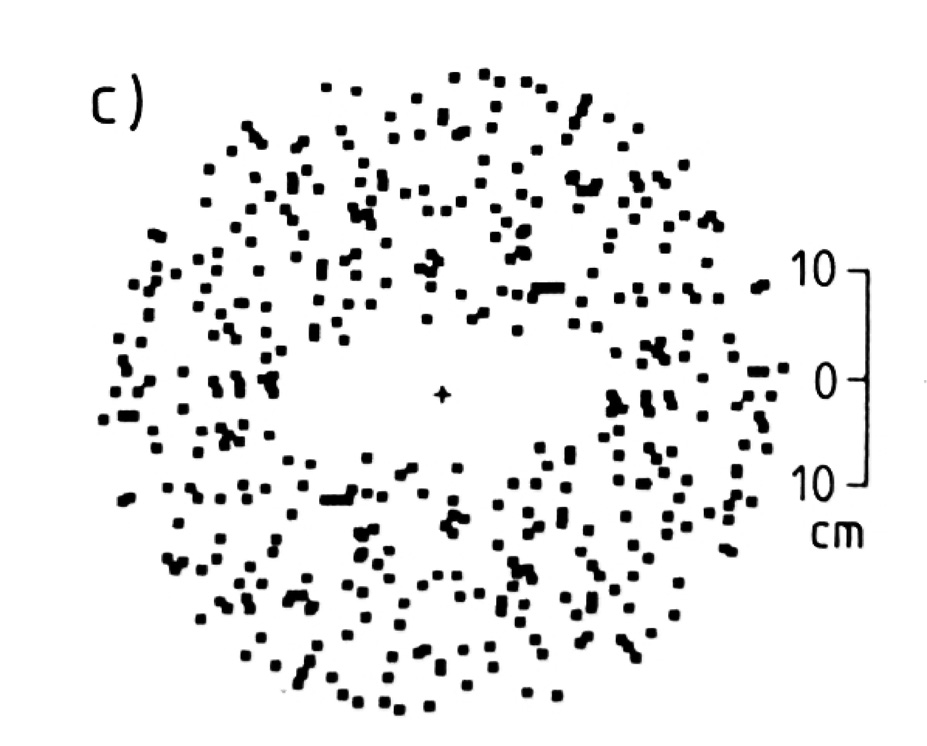
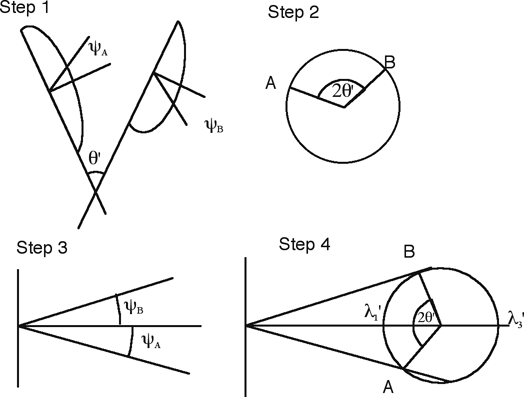
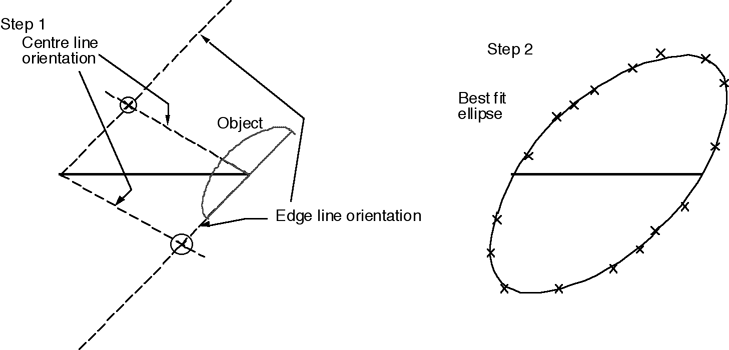
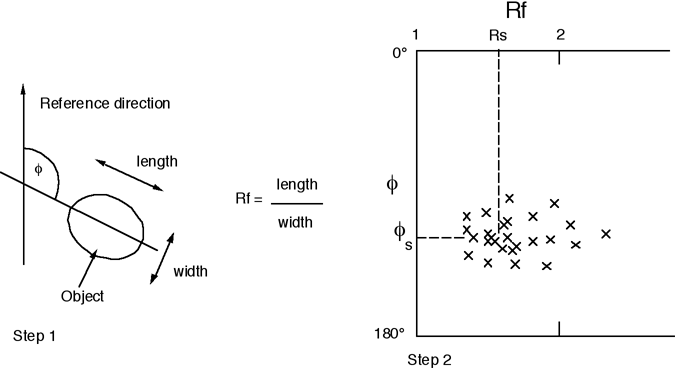
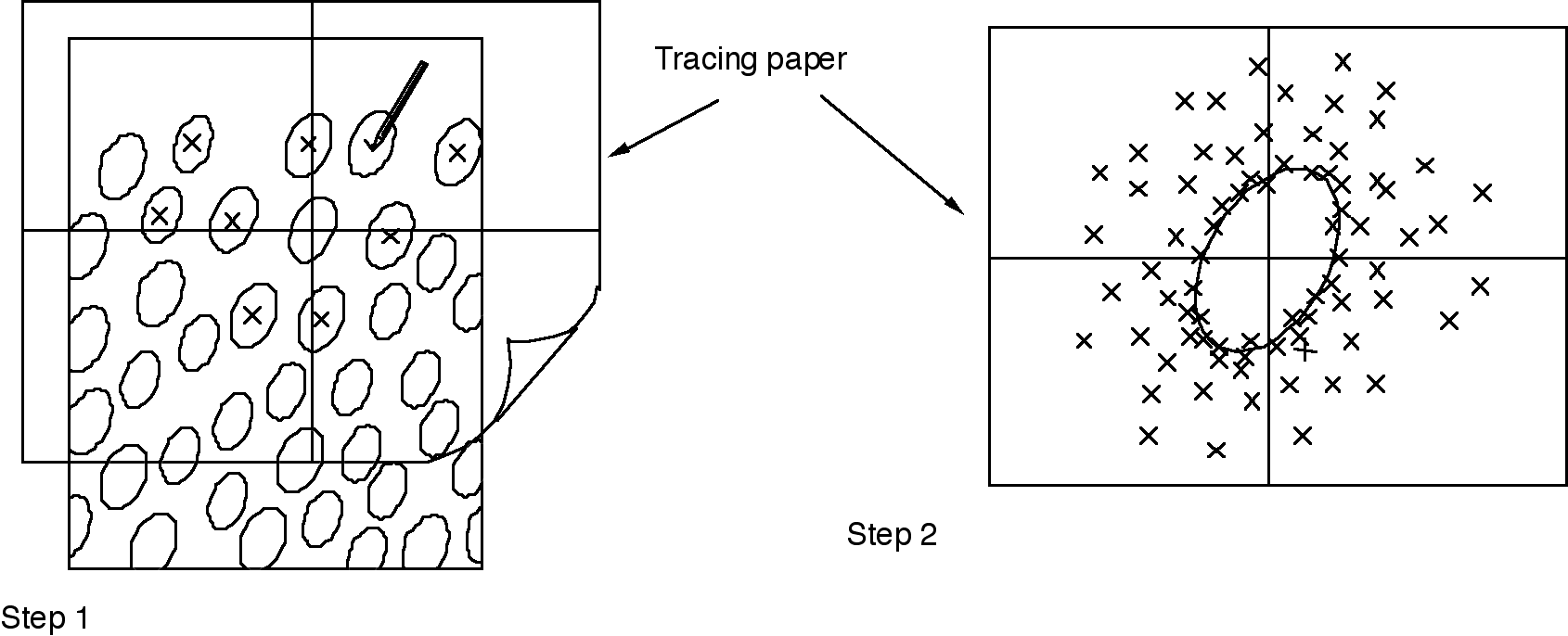
Diagrams illustrating the Fry (centre to centre) method of strain analysis and Principle of the Rf-phi plot for deformed elliptical objects. Ramsay, J. G., and Huber, M. I., 1983, The Techniques of Modern Structural Geology. Volume 1: Strain Analysis: London, Academic Press, 307 p. Reproduced under license from Cancopy; further reproduction prohibited
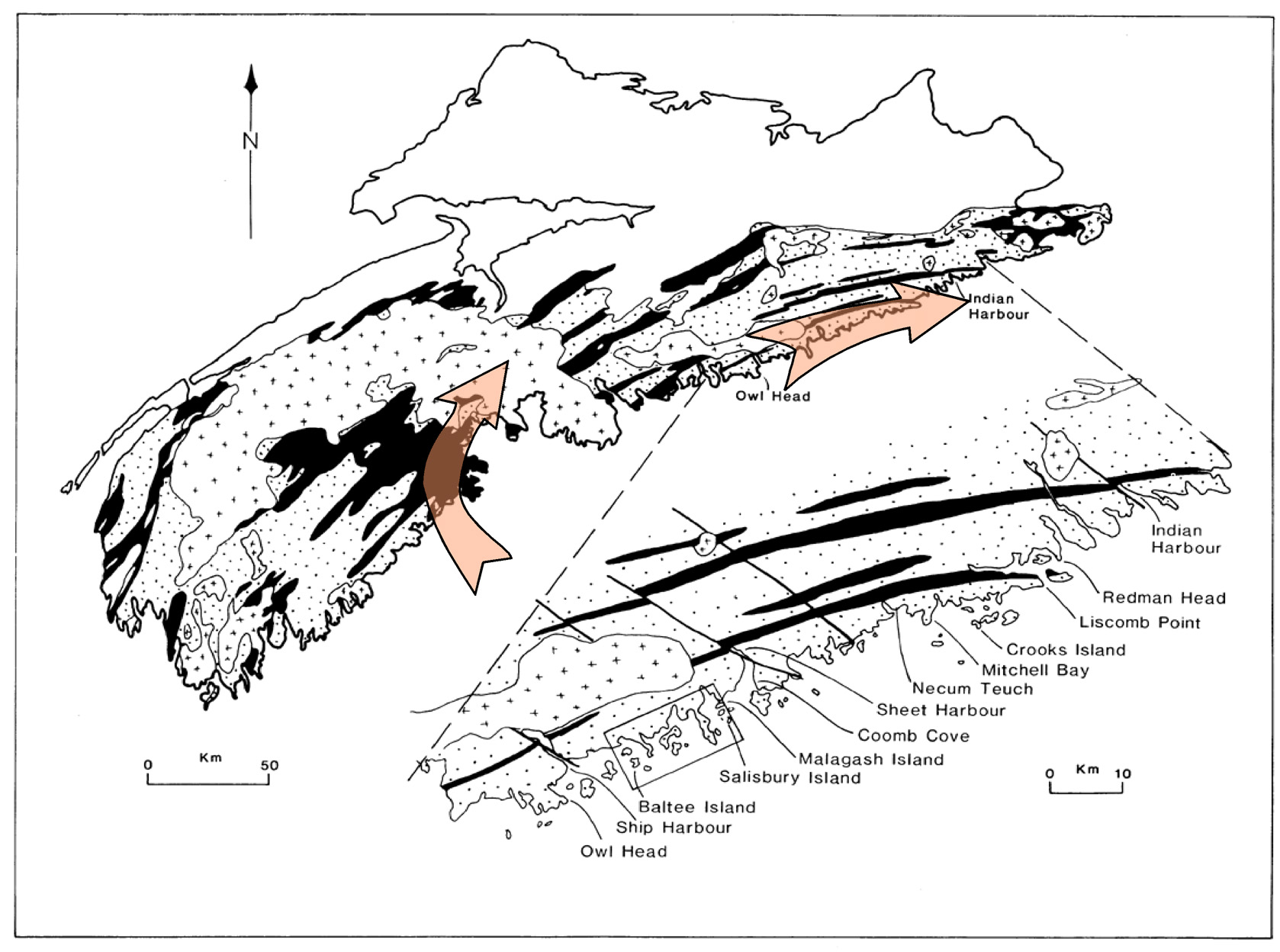
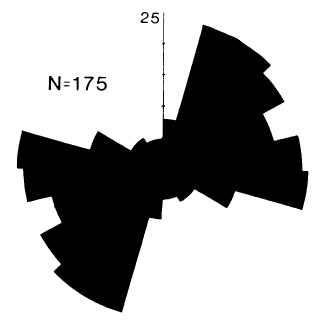
Paleocurrent study of deformed turbidite basin: Cambrian-Ordovician Meguma Group, NS
 |
|
|
|
|
 |
|
 |
|
|
 |
|
Map shows distribution of Goldenville sandstones (stipple) and Halifax slate (black)
a) All accumulated paleocurrent data treated as non-polar
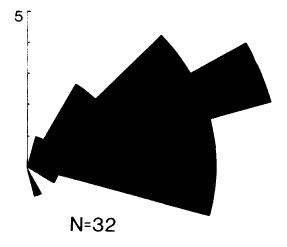
b) Same dataset as (a) after removal of strain
c) Polar data only (mainly flutes) extracted from (b) |
|
|
|
|
|
|
|
Paleocurrent study: Meguma Group of Nova Scotia, south shore, showing effect of strain removal
Cross-section showing strain variation in Morcles Nappe, Swiss Alps. After Ramsay, J. G., and Huber, M. I., 1983, The Techniques of Modern Structural Geology. Volume 1: Strain Analysis: London, Academic Press, 307 p. Reproduced under license from Cancopy; further reproduction prohibited
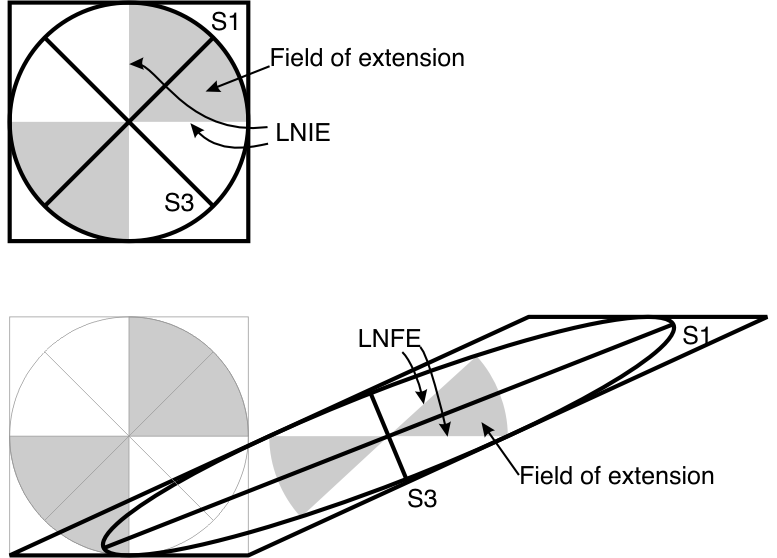
Prolate ellipsoid with surfaces of no extension
Diagram showing range of shapes of strain ellipsoid (Flynn plot). After Ramsay, J. G., and Huber, M. I., 1983, The Techniques of Modern Structural Geology. Volume 1: Strain Analysis: London, Academic Press, 307 p. Reproduced under license from Cancopy; further reproduction prohibited.
Diagrams showing fabrics developed by deformation of random populations of passive markers. Ramsay, J. G., and Huber, M. I., 1983, The Techniques of Modern Structural Geology. Volume 1: Strain Analysis: London, Academic Press, 307 p. Reproduced under license from Cancopy; further reproduction prohibited
Diagrams showing ideal folds displaying Tangential Strain and Flexural Slip. After Van Der Pluijm, B.A. and Marshak S. 2004, Earth Structure 2nd Edition W.W. Norton. Reproduced under license from CANCOPY; sale and further reproduction prohibited
|
|
|
|
Re-orienting paleocurrents using the strain ellipse
|
|
 |
|
|
|
|
|
Reciprocal deformation matrix
|
|
|
 |
|
|
|
Small increment of simple shear
|
|
|
is equal to.....
|
|
|
 |
|
|
a small increment of pure shear....
|
|
|
|
....and a small increment of rotation
|
|
|
|
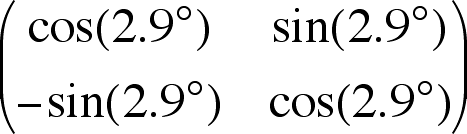 |
|
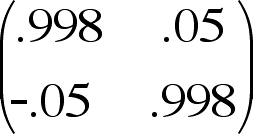 |
|
|
or
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Progressive simple shear
|
|
 |
|
|
|
|
|




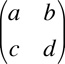
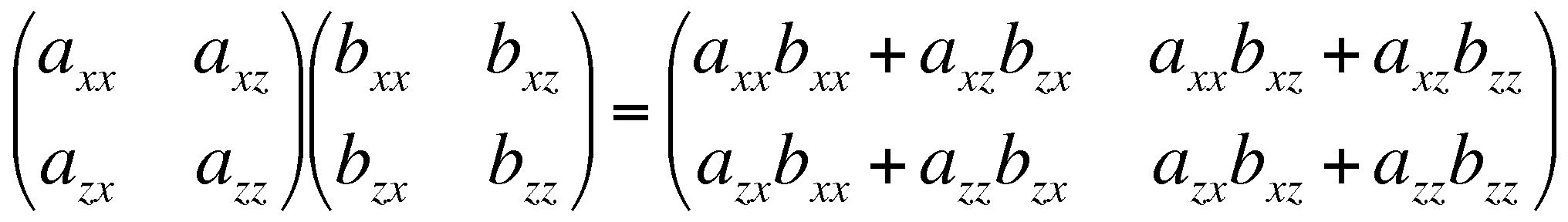
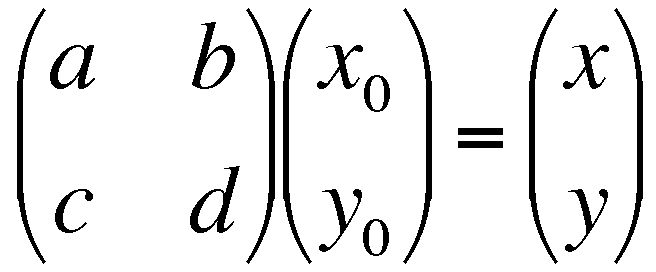
 The matrix that does nothing
The matrix that does nothing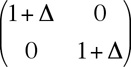 A matrix that describes a simple dilation
A matrix that describes a simple dilation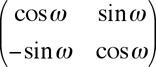 A rotation clockwise about the origin
A rotation clockwise about the origin 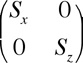 A pure strain with strain axes parallel to x and y
A pure strain with strain axes parallel to x and y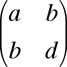 A general pure strain
A general pure strain 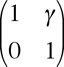 A simple shear parallel to x
A simple shear parallel to x