Liquids flow as soon as a shear stress is applied, and the rate of shear strain is proportional to the stress. The constant of proportionality is called the viscosity. Some solid rocks behave in this way during deformation at relatively low stress and strain rates; the actual viscosities are very high.
The equation for viscous flow is
![]()
or ![]()
where η is the viscosity and σd is the differential stress σ1 - σ3
Visco-elastic are essentially elastic, but show a delayed response to stress as the material flows into its elastically deformed state.
Elastico-viscous material deforms viscously at low strain rates and low stress, flowing like a liquid, but when the strain rate increases, elastic (and eventually brittle) behaviour takes over. Some rocks at high temperatures exhibit behaviour that it approximately elastico-viscous. Silly putty is an every-day example.
We may imagine a material which is rigid or elastic at low stress but which starts to flow easily when a fixed yield stress is reached.
![]()
This is described as ideal plastic or Von Mises behaviour. The stress within the material can never exceed the yield stress because the material flows at whatever speed is necessary to get out of the way of the applied stress. Obviously this is an idealized model for flow, but it approximates some types of materials, especially if the strain rate is kept low.
Some geologic materials undergo a transition from brittle to plastic behaviour as depth increases. The failure envelope for such a material appears as in VDPM 06.21a
Many minerals do not show Newtonian behaviour. Instead, the apparent viscosity changes with strain rate. Some materials follow what is called a power law relationship.
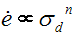
Under other conditions, it is found that the strain rate is proportional to an exponential function of the stress.
The exponential function is based on the number e = 2.718... raised to some power, but we are already using e for strain so it's better to write the exponential function thus
![]()