Kinematics of folding

In the following sections we apply balancing techniques to three common fold geometries in thrust belts.

Kinematics of fault-bend folding

Fault-bend folds have been well-known since the 50s and 60s. Typically in thrust belts we assume that the HW is deformed and the FW remains rigid. This assumption has been criticized on the grounds that it does not work well at outcrop-scale.

Compare the animation with this photograph of fault-bend folding at a thrust ramp in Carboniferous rocks from Nova Scotia

Common kinematic models make the assumption that ramps and flats are angular and use the kink construction.

There are two general cases:

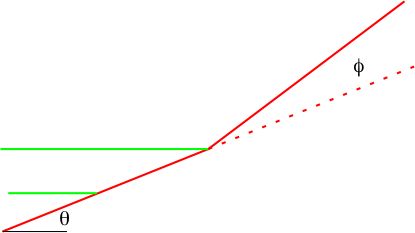
• Convex-up fault bends from steep dip (θ theta) to gentle (θ - φ where phi is the dip change)
  Step 1: Fault with dip q and concave-up bend through angle f
  
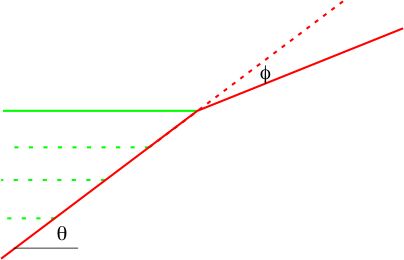
  Step 2: hangingwall displaced upward creating a "gap" that must be filled.
  
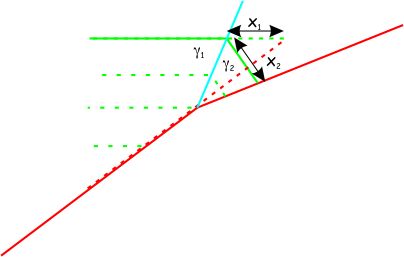
  Step 3: hangingwall collapses filling "gap", creating a fold axial trace oriented such that:
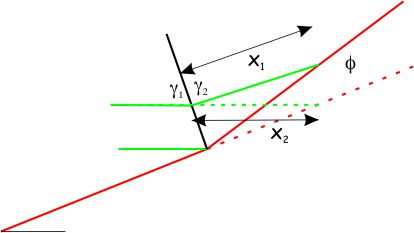
  γ1 = γ2 (kink construction constraint) and
  x1 = x2 (line-length balancing constraint)
  
• Concave-up fault bends from gentle dip (θ theta) to steep (θ + φ where phi is the dip change)
  Step 1: Fault with dip q and concave-up bend through angle f
  
  Step 2: hangingwall displaced upward creating an "overlap" that must be avoided
  
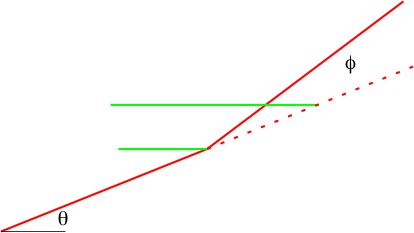
  Step 3: hangingwall raised avoiding "overlap", creating a fold axial trace oriented such that:
  γ1 = γ2 (kink construction constraint) and
  x1 = x2 (line-length balancing constraint)
  

Suppe solved the trigonometry and plotted half-interlimb angle γ against θ for different values of φ.

[Suppe and Medwedef graph]

Both solutions are much simplified if the flats are accurately bed-parallel. Then θ = 0 and φ = ramp dip.

Then, for the concave-up case the fold axial plane just bisects the ramp angle. For a convex-up bend the trigonometry is still complex, though the case of a 30° ramp angle is simple, giving γ = 60°.

Suppe graph for simple case

Note that for a flat-ramp-flat system, the folds evolve through two distinct configurations, depending on whether the HW ramp overlaps the FW ramp.

animation of fault-bend fold

In general, just the form of a fault-bend fold doesn't allow us to predict the depth of a décollement, but given the position of the décollement we can trace the route of a thrust through the subsurface and solve the geometry.

Kinematics of detachment folding

Because of the nature of detachment folding, where the core of each fold is filled by highly thickened shale, evaporite, or other incompetent rock, area balancing is almost always required. The kink construction tends to produce unrealistic-looking sections of detachment folds. Sometimes we can use the arc (Busk) construction to get an estimate of the depth to detachment.

Area relationships at detachment folds (assuming balancing relationships hold)

If thickness of detached layer is d, and excess cross-section area of fold is A, then

dx₁-dx₂=A or d(x₁-x₂)=A

where x₁ is the slip at the hinterland side and x₂ is slip at foreland side.

Diagram shows the relationship between areas in balancing a detachment fold.

Kinematics of fault-propagation folding

Fault-propagation folding is the most complicated. It combines elements of detachment folding (in that the fault loses displacement in the direction of transport) and fault-bend folding (because the fold occurs on a ramp).

The area-balancing techniques for detachment folding, described above, also apply to fault-propagation folds.

However, it's also possible to apply line-length balancing. Notice that for a fault-propagation fold to balance, the shortening by folding in strata higher than the fault tip must be exactly the same as the shortening by thrusting at the basal detachment.

Suppe has solved the rather complex trigonometrical problem of balancing an idealized fault-propagation fold by kink construction. One simple result of this complex problem is that the backlimb of the fold is exactly twice the slip on the fault. The relationships between the various angles are shown in a graph.

[Graph showing angular relationships in simple fault-propagation fold]

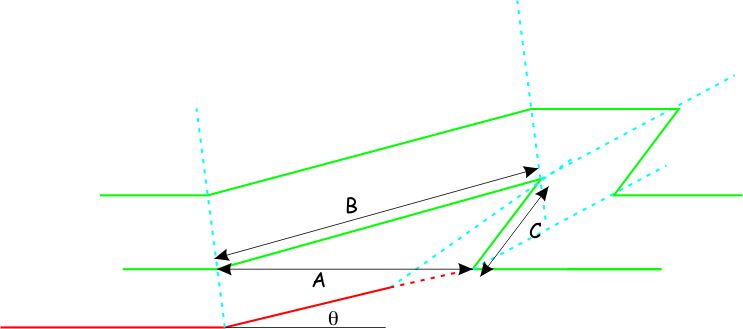
To sketch a fault-bend fold using the kink construction

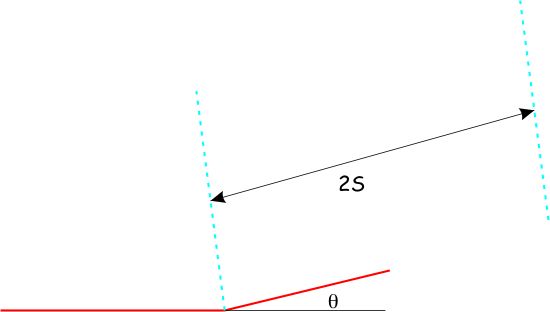
• First draw a flat and a ramp having a length equal to the amount of slip s, to a point X.
• Bisect the angle at the base of the ramp to sketch a fold axial surface. Sketch another fold axial surface, ahead of the first by a distance 2s.
  
• A third fold axial surface extends from X, more steeply than the ramp (making an angle γ* to the ramp). Where it intersects the second axial surface, mark a hinge point H. To make the construction work exactly, you will need to look up the angle γ* from a graph.
  
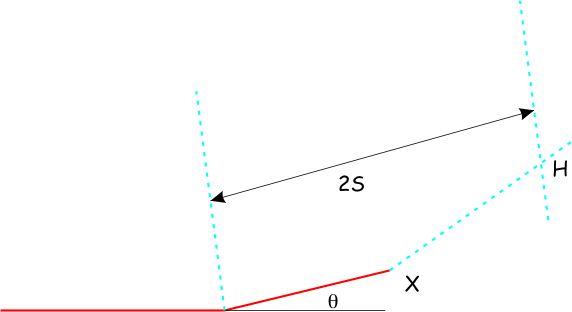
• Construct the folded horizon that passes through H. This is the lowest horizon unaffected by faulting (only folding).
  
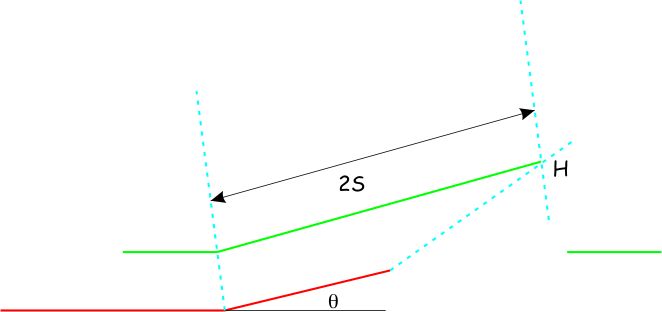
• Next, extend the ramp forward to a tip point T that lies on the same horizon as H. Between X and T, the fault slip declines linearly to zero.
  
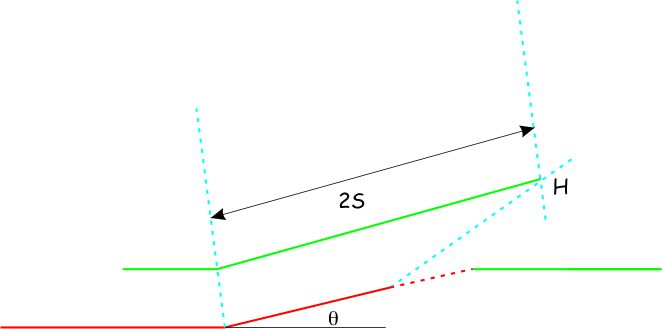
• Construct the forelimb between H and T. If you have used the precise value of γ* then axial surface 3 should bisect the angle of the antiform you have just completed
  
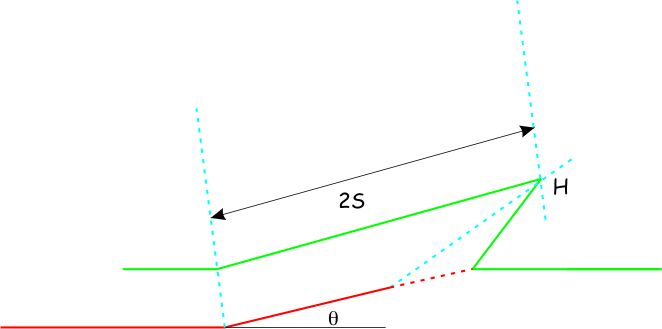
• Draw a fourth axial surface bisecting the angle between the forelimb and the horizontal strata ahead of the fold. A fifth axial surface extends forward from H at the same angle. Construct higher strata with a horizontal upper limb between axial surfaces 3 and 5.
  
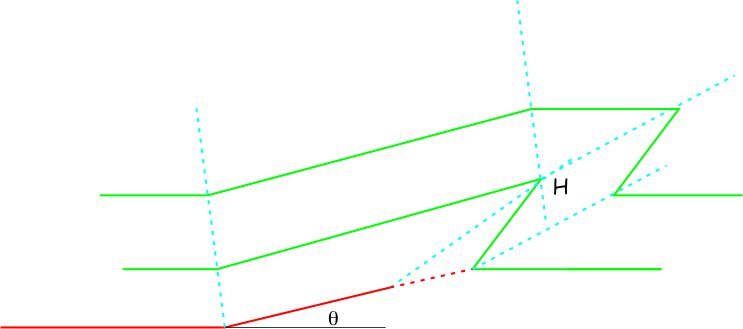
• For the fold to balance correctly, all the axial surfaces should bisect the folds, and the shortening by folding (B+C-A) in the top of the section should exactly balance shortening by thrusting (S) at the bottom. Suppe and Medwedeff solved the complex trigonometric problem to make this happen and plotted the results. To make the construction work exactly, the angle γ* should be read from their graph.
  

Although geometrically 'perfect', this geometric model has been questioned on kinematic grounds. For a fault-propagation fold to maintain this geometry while the fault propagates (i.e. to have self-similar growth), it's necessary for strata to continuously roll through the fold axial surface, distorting and un-distorting as it goes. Examination of real folds seldom shows evidence that the rocks have been through this type of strain history. Hence alternative geometries have been proposed, in which axial surfaces remain fixed for periods of time. For these to work, it's necessary to relax the strict constraints of the kink construction, and to use area balancing where layers change thickness.

[Example]