I. Vectors and matrices

Scalar quantities

Scalar quantities are quantities like mass, hardness, represented by one number

Vector quantities

Vector quantities have magnitude and direction.

Represented by an arrow - sketch

Good review of vectors in T&M p132

In 2D require two numbers to specify (e.g. azimuth and length, x and y coordinates)

In 3D require 3 numbers (eg plunge trend and length, x, y and z coordinates)

Sometimes it's useful to define vectors that have unit magnitude. E.g. plunge and trend measurements have direction but no magnitude. We arbitrarily treat them as vectors one unit long

Represented bold in text, in handwriting with line over top

Vector components

If we have a coordinate system its convenient to represent vectors as three components by projecting onto three axes eg:

east
north
up

x
y
z

x1
x2
x3

Diagram of components of a vector

If magnitude is F, and angles to x1, x2, x3 axes are q1 q2 q3 then the magnitudes of the three components are

f₁ = F cos q1
f₂ = F cos q2
f₃ = F cos q3

Note that to get back to magnitude given 3 components we use F² = f₁²+f₂²+f₃²

Unit vectors, direction cosines

For geological measurements that have orientation but no magnitude, we use a magnitude of 1

The magnitudes of the three components are

cos q1
cos q2
cos q3

Converting plunge and trend to direction cosines:

(diagram showing derivation of components)

l = sin T cos P
m = cos T cos P
n = -sin P

Converting direction cosines to plunge and trend:

Trend depends on how the inverse tan function is implemented. Most calculators give inverse tan between -90 and +90

T =Tan^-1(m/l) if l is positive or
T =Tan^-1(m/l) + 180 if l is negative
P =Sin^-1(n)

Vector addition

Vectors are added by parallelogram rule

Diagram of parallelogram rule

Or by adding components

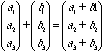
Vector addtion is a convenient way to represent a translation. If objects have move, and we represent each point in the object by a pair of coordinates, then if we add the same vector to all the points, we move the object to a new location - process called translation.

Vector dot product: angle between two vectors

Vectors are multiplied a.b = a.b cos q

where a is magnitude of a, and q is angle between them

To find the dot product given components we use

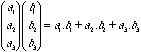
Hence if we calculate this we can find cos q

Especially easy for a unit vectors where a.b = cos q

Vector cross product: line perpendicular to two vectors

Vector cross product is a vector

Perpendicular to two starting vectors, with magnitude equal to the area enclosed by a parallelogram defined by the two vectors. (The three form a right handed set)

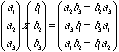
This represents a convenient way to calculate the line perpendicular to two other lines.

Note that axb is in the opposite direction to bxa

Matrices

Matrix components

Some geological quantities require more information than a simple scalar or vector. For example, the state of stress at a point requires three values of principal stresses, plus the plunge and trend of one, plus the pitch of a second in the plane perpendicular to the first - six numbers in all.

Similarly, to describe the deformation that has occurred at a point in a body of rock, we need to specify the shape and orientation of a strain ellipsoid - requires a similar number of numbers. These are examples of second order tensors (a vector is actually a first order tensor). Just as we used a column of three numbers for a vector, we use a table of numbers for a second order tensor.

Second order tensors describe properties that vary with direction - refractive index in an anisotropic crystal, the state of stress at a point in the earth, the strain that has affected a point within the earth as rocks are deformed. All these quantities can also be represented by ellipsoids - this is not a coincidence.

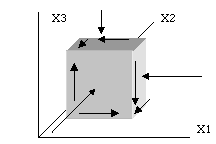
In the diagram there are nine stress arrows, three normal to the faces of the cube and six parallel to the faces. These are combined in a matrix that represents the state of stress at a point. The stress tensor.

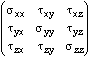
Matrix addition

We will work in two dimensions for now...

Matrix multiplication

Note: elements of row i in first matrix are multiplied by elements of column j in second matrix. these products are added to get element ij in product

Sometimes this is written

a_ip . b_pj = c_ij

Note - not commutative A.B is not B.A

Non square matrices can be multiplied provided the rows of the first matrix are the same length as the columns of the second.

Hence we may multiply a vector by a matrix

Example - matrices and  finite strain

To illustrate use of matrices, we will multiply some vectors, representing points on a graph, all by the same matrix F

Plotting as a class exercise here requires graph paper

Choose four points at the corner of a unit square.

Matrix F will be

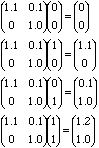
So we can use a matrix to describe any finite homogeneous deformation - at least the dilation, distortion, and rotation part. Can't describe a translation because we can't move the origin.

Symmetric and skew-symmetric matrices

symmetric

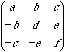skew-symmetric

Transpose of a matrix

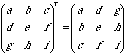
The matrix that does nothing

is called Kronecker's delta or

A = A = A

Determinant

Special number that describes a matrix is the determnant |A|. In 2 dimensions determnant |A|= a₁₁a₂₂-a₁₂a₂₁

The determinant of the deformation tensor represents the dilation: the new volume divided by the old volume.

Inverse of a matrix

A^-1 is defined such that AA^-1=A^-1A=d

For a 2x2 matrix A^-1 = A^T / |A|