A quick introduction to vector quantities

Vector quantities have magnitude and direction.

Represented by an arrow

In 2D require two numbers to specify (e.g. azimuth and length, x and y coordinates)

In 3D require 3 numbers (eg plunge trend and length, x, y and z coordinates)

Sometimes it's useful to define vectors that have unit magnitude. E.g. plunge and trend measurements have direction but no magnitude. We arbitrarily treat them as vectors one unit long

Represented bold in text, in handwriting with line over top

Vector components

If we have a coordinate system its convenient to represent vectors as three components by projecting onto three axes eg:

east
north
up

x
y
z

x1
x2
x3

If magnitude is F, and angles to x1, x2, x3 axes are θ1 θ2 θ3 then the magnitudes of the three components are

f₁ = F cos θ1
f₂ = F cos θ2
f₃ = F cos θ3

Note that to get back to magnitude given 3 components we use F² = f₁²+f₂²+f₃²

Unit vectors, direction cosines

For geological measurements that have orientation but no magnitude, we use a magnitude of 1

The magnitudes of the three components are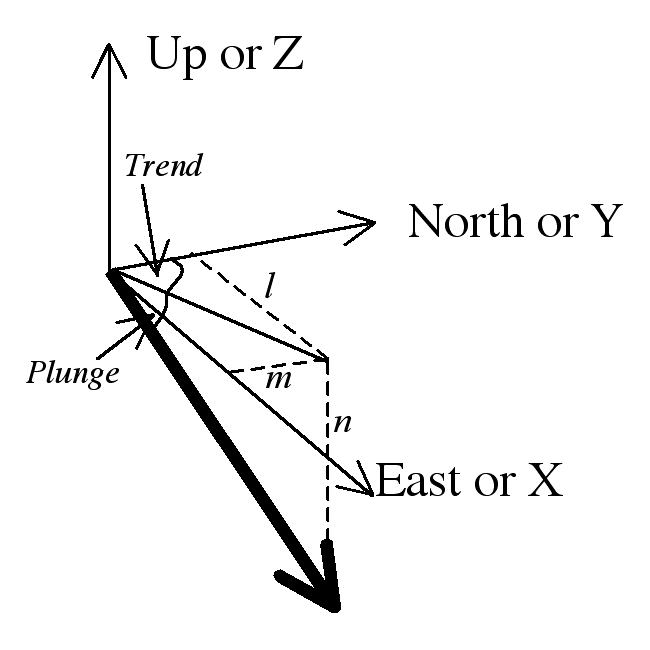

cos θ1
cos θ2
cos θ3

Converting plunge and trend to direction cosines:

l = sin T cos P
m = cos T cos P
n = -sin P

Trend depends on how the inverse tan function is implemented. Most calculators give inverse tan between -90 and +90

T =Tan^-1(m/l) if l is positive or
T =Tan^-1(m/l) + 180 if l is negative
P =Sin^-1(n)

Vector calculations

Vector magnitude

The magnitude of vector a, represented as |a| or just a  is given by |a|= √(a_x²+ a_y²_­+ a_z²)

Vector sum

Vectors are added by adding their components.

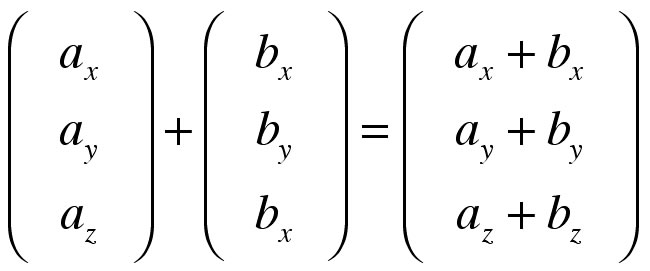
Alternatively the calculation can be carried out graphically using the well known parallelogram rule.

Vector dot product: angle between two lines

For two vectors a and b the dot product

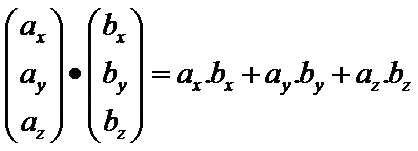
a.b = abcosθ where a and b are the magnitudes of a and b and θ is the angle between the vectors.

For unit vectors â.b = cosθ

So, we can use the dot product to calculate the angle between two lines.

Vector cross product: line perpendicular to two lines

For two vectors a and b the cross product a x b = c is given by

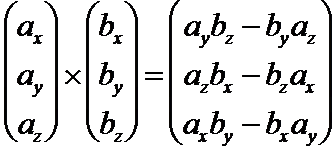
The cross product is a third vector mutually perpendicular to the first two, where a, b and c form a right-handed set (i.e. they have the same relative arrangement as x, y and z).  The magnitude of a x b is absinθ.

Hence we can use the cross product to find the line perpendicular to two other lines. 

Caution: even if a and b are unit vectors, the magnitude of c is not equal to one, and therefore its components are not direction cosines.  To convert them to direction cosines, divide each by the magnitude of c, represented as |c|  or c = √(c_x²+ c_y²_­+ c_z²)